深層結構學習或分層學習或簡稱深層學習是機器學習方法家族的一部分,它們本身是人工智慧更廣泛領域的一個子集。
深度學習是一類利用多層非線性處理單元進行特徵提取和轉換的機器學習算法。每個連續的層都使用前一層的輸出作爲輸入。
深層神經網絡、深層信念網絡和遞歸神經網絡已被應用於計算機視覺、語音識別、自然語言處理、音頻識別、社會網絡濾波、機器翻譯等領域,以及生物信息學,在那裡他們產生的結果可以與人類專家相媲美,在某些情況下甚至優於人類專家。
深度學習算法與網絡&負;
基於無監督學習的多層次特徵或數據表示。高級特徵是從低級特徵派生而來,形成層次表示。
使用某種形式的梯度下降進行訓練。
Python Deep Learning - Environment
在本章中,我們將了解爲Python深入學習設置的環境。我們必須安裝以下軟體來製作深度學習算法。
- Python 2.7+
- Scipy with Numpy
- Matplotlib
- Theano
- Keras
- TensorFlow
強烈建議通過Anaconda發行版安裝Python、NumPy、SciPy和Matplotlib。所有這些包裹都有。
我們需要確保不同類型的軟體安裝正確。
讓我們轉到命令行程序,輸入以下命令−
$ python Python 3.6.3 |Anaconda custom (32-bit)| (default, Oct 13 2017, 14:21:34) [GCC 7.2.0] on linux
接下來,我們可以導入所需的庫並列印它們的版本;
import numpy print numpy.__version__
Output
1.14.2
Installation of Theano, TensorFlow and Keras
在開始安裝軟體包之前,我們需要確認是否安裝了pip。水蟒的包裝管理系統稱爲pip。
要確認pip的安裝,請在命令行中鍵入以下內容−
$ pip
一旦確認pip的安裝,我們就可以通過執行以下命令來安裝TensorFlow和Keras−
$pip install theano $pip install tensorflow $pip install keras
通過執行下面的代碼行來確認是否安裝了ano−
$python –c 「import theano: print (theano.__version__)」
Output
1.0.1
通過執行以下代碼行確認Tensorflow的安裝−
$python –c 「import tensorflow: print tensorflow.__version__」
Output
1.7.0
通過執行以下代碼行來確認路緣石的安裝;
$python –c 「import keras: print keras.__version__」 Using TensorFlow backend
Output
2.1.5
Python Deep Basic Machine Learning
人工智慧是使計算機能夠模擬人類認知行爲或智能的任何代碼、算法或技術。機器學習(ML)是人工智慧的一個子集,它使用統計方法使機器能夠通過經驗學習和改進。深度學習是機器學習的一個子集,使得多層神經網絡的計算成爲可能。機器學習被看作是淺層學習,而深層學習被看作是抽象的層次學習。
機器學習涉及廣泛的概念。下面列出了這些概念;
- supervised
- unsupervised
- reinforcement learning
- linear regression
- cost functions
- overfitting
- under-fitting
- hyper-parameter, etc.
在監督學習中,我們學習從標記數據預測值。一種ML技術有助於分類,目標值是離散值,例如貓和狗。機器學習中的另一個可能會有幫助的技術是回歸。回歸作用於目標值。目標值是連續值;例如,可以使用回歸分析股市數據。
在無監督學習中,我們從沒有標記或結構的輸入數據進行推理。如果我們有一百萬份醫療記錄,我們必須弄清楚它的意義,找到潛在的結構、異常點或檢測異常,我們就使用聚類技術將數據劃分爲廣泛的聚類。
數據集分爲訓練集、測試集、驗證集等。
2012年的突破,使深度學習理念凸顯。一種算法使用2個gpu和大數據等最新技術成功地將100萬張圖像分爲1000類。
Relating Deep Learning and Traditional Machine Learning
傳統機器學習模型面臨的主要挑戰之一是一個稱爲特徵提取的過程。程式設計師需要明確地告訴計算機需要注意的特性。這些功能將有助於作出決定。
將原始數據輸入到算法中很少奏效,因此特徵提取是傳統機器學習工作流的關鍵部分。
這給程式設計師帶來了巨大的責任,而算法的效率在很大程度上取決於程式設計師的創造力。對於複雜的問題,如物體識別或手寫識別,這是一個巨大的問題。
深度學習具有學習多層次表示的能力,是幫助我們自動提取特徵的少數方法之一。可以假設較低層執行自動特徵提取,幾乎不需要程式設計師的指導。
Artificial Neural Networks
人工神經網絡,簡稱神經網絡,並不是一個新的概念。它已經存在了大約80年。
直到2011年,隨著新技術的應用、巨大的數據集可用性和強大的計算機的出現,深神經網絡才開始流行起來。
神經網絡模擬一個神經元,它有樹突、核、軸突和終末軸突。
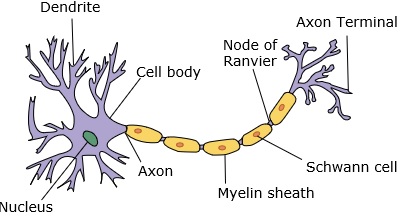
對於一個網絡,我們需要兩個神經元。這些神經元通過一個樹突和另一個軸突終末之間的突觸傳遞信息。
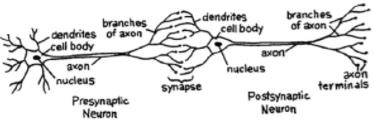
人工神經元的可能模型看起來是這樣的;
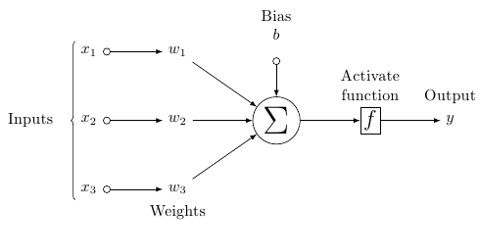
神經網絡如下所示;
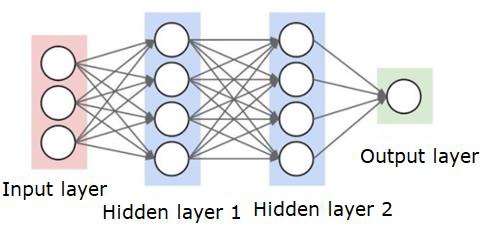
圓是神經元或節點,它們在數據上的功能和連接它們的線/邊是傳遞的權重/信息。
每一列都是一層。數據的第一層是輸入層。然後,輸入層和輸出層之間的所有層都是隱藏層。
如果你有一個或幾個隱藏層,那麼你就有一個淺層神經網絡。如果你有很多隱藏層,那麼你就有一個深層的神經網絡。
在這個模型中,你有輸入數據,你給它稱重,然後把它傳遞給神經元中的函數,這個函數叫做閾值函數或激活函數。
基本上,它是所有值與某個值比較後的總和。如果觸發一個信號,則結果爲(1)out,或者不觸發任何信號,則爲(0)。然後加權並傳遞給下一個神經元,然後運行同樣的函數。
我們可以用乙狀結腸(s形)作爲激活函數。
至於權重,它們只是隨機開始的,而且每個節點/神經元的輸入都是唯一的。
在一個典型的「前饋」,最基本的神經網絡類型,你有你的信息直接通過網絡,你創建,你比較的輸出,你希望的輸出將一直使用你的樣本數據。
從這裡開始,您需要調整權重,以幫助您獲得與所需輸出匹配的輸出。
通過神經網絡直接發送數據的行爲稱爲a前饋神經網絡
我們的數據從輸入,到層,按順序,然後到輸出。
當我們向後移動並開始調整權重以最小化損失/成本時,這稱爲反向傳播
這是一個優化問題。在實際應用中,神經網絡需要處理數十萬個變量,或數百萬個或更多的變量。
首先採用隨機梯度下降法作爲優化方法。現在,有像AdaGrad、Adam Optimizer等選項。不管怎樣,這都是一個龐大的計算操作。這就是爲什麼神經網絡被擱置了半個多世紀的原因。直到最近,我們才有能力和架構在我們的機器甚至考慮做這些操作,並適當大小的數據集來匹配。
對於簡單的分類任務,神經網絡在性能上與K近鄰等簡單算法比較接近。當我們有更大的數據和更複雜的問題時,神經網絡的真正效用就實現了,這兩個問題都優於其他機器學習模型。
Deep Neural Networks
深度神經網絡(DNN)是一種在輸入層和輸出層之間具有多個隱含層的神經網絡。與淺層ann相似,DNNs可以模擬複雜的非線性關係。
神經網絡的主要目的是接收一組輸入,對它們進行逐步複雜的計算,並給出輸出以解決實際問題,如分類。我們限制自己使用前饋神經網絡。
我們在一個深網絡中有一個輸入,一個輸出和一個序列數據流。
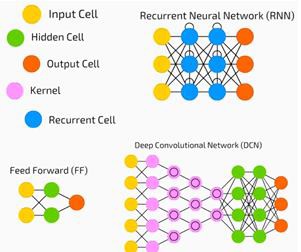
神經網絡廣泛應用於有監督學習和強化學習問題。這些網絡基於一組相互連接的層。
在深度學習中,隱藏層的數量,大多是非線性的,可以很大;比如說大約1000層。
DL模型比普通的ML網絡產生更好的結果。
我們主要採用梯度下降法對網絡進行優化和損失函數最小化。
我們可以使用Imagenet,一個數百萬數字圖像的存儲庫,將數據集分類爲貓和狗等類別。DL網絡除了用於靜態圖像之外,越來越多地用於動態圖像、時間序列和文本分析。
數據集的訓練是深度學習模型的重要組成部分。另外,反向傳播算法是訓練DL模型的主要算法。
DL處理具有複雜輸入輸出變換的大型神經網絡的訓練。
DL的一個例子是將照片映射到照片中的人的名字,就像他們在社交網絡上那樣,用短語描述圖片是DL的另一個最新應用。
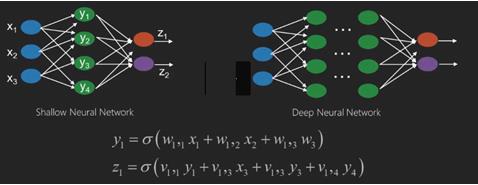
神經網絡是具有像x1、x2、x3等輸入的函數,在兩個(淺網絡)或幾個中間操作(也稱爲層(深網絡))中轉換爲像z1、z2、z3等輸出。
權重和偏差會隨著層的變化而變化。「w」和「v」是神經網絡各層的權值或突觸。
深度學習的最佳用例是有監督學習問題,在這裡,我們有大量的數據輸入和期望的輸出。
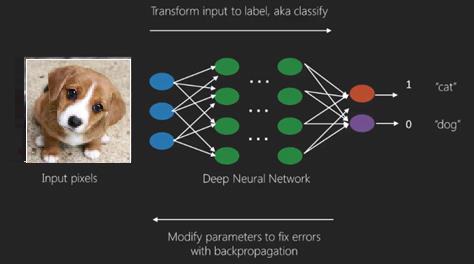
在這裡我們應用反向傳播算法得到正確的輸出預測。
深度學習最基本的數據集是MNIST,一個手寫數字集。
利用Keras對卷積神經網絡進行深度訓練,對該數據集中的手寫數字圖像進行分類。
神經網絡分類器的啓動或激活產生分數。例如,要將患者分爲病患和健康者,我們會考慮身高、體重和體溫、血壓等參數。
高分表示病人生病,低分表示病人健康。
輸出層和隱藏層中的每個節點都有自己的分類器。輸入層接受輸入並將其分數傳遞給下一個隱藏層以進行進一步的激活,這一直持續到達到輸出爲止。
這種從輸入到輸出的前進方向從左到右的過程稱爲前進傳播
神經網絡中的信用分配路徑(CAP)是從輸入到輸出的一系列變換。CAPs闡述了輸入和輸出之間可能的因果關係。
一個給定的前饋神經網絡的覆蓋深度,或者覆蓋深度是隱藏層的數量加上一個作爲輸出層。對於遞歸神經網絡,其中一個信號可以通過一個層傳播幾次,上限深度可能是無限的。
Deep Nets and Shallow Nets
淺層學習和深層學習沒有明確的深度閾值,但對於具有多個非線性層的深層學習,CAP必須大於2。
神經網絡中的基本節點是模仿生物神經網絡中神經元的感知。然後我們有多層感知或MLP。每一組輸入都由一組權重和偏差進行修改;每條邊都有一個唯一的權重,每個節點都有一個唯一的偏差。
神經網絡的預測精度取決於其權重和偏差
提高神經網絡精度的過程稱爲訓練,將前向支撐網的輸出與已知的正確值進行比較。
成本函數或損失函數是產生的產出與實際產出之間的差額。
訓練的目的是使數百萬個訓練實例的訓練成本儘可能小,爲此,網絡會調整權重和偏差,直到預測與正確的輸出匹配。
一旦訓練好,神經網絡每次都有可能做出準確的預測。
當模式變得複雜,你想讓你的計算機識別它們時,你必須使用神經網絡,在如此複雜的模式場景中,神經網絡的性能要優於其他競爭算法。
現在有GPU可以比以前更快地訓練他們。深層神經網絡已經在人工智慧領域掀起革命
事實證明,計算機擅長重複計算和遵循詳細的指令,但不善於識別複雜的模式。
如果存在簡單模式的識別問題,支持向量機(svm)或邏輯回歸分類器可以很好地完成這項工作,但隨著模式複雜度的增加,沒有辦法只能使用深層神經網絡。
因此,對於像人臉這樣的複雜模式,淺層神經網絡失效了,除了更深層的神經網絡之外別無選擇。深度網能夠通過將複雜的模式分解爲簡單的模式來完成它們的工作。例如,人臉;adeep網絡會使用邊緣來檢測嘴脣、鼻子、眼睛、耳朵等部位,然後將這些部位重新組合在一起形成人臉
正確預測的準確性變得如此精確,以至於最近在谷歌模式識別挑戰賽上,一個深網打敗了一個人。
這種由多層感知器組成的網絡的想法已經存在了一段時間;在這個領域,深層網絡模擬了人腦。但它的一個缺點是它們需要很長時間來訓練,這是一個硬體限制
然而,最近的高性能gpu能夠在一周內訓練出如此深的網;而快速的cpu可能需要數周甚至數月的時間來訓練。
Choosing a Deep Net
如何選擇深網?我們必須決定是要建立一個分類器,還是要在數據中尋找模式,以及是否要使用無監督學習。爲了從一組未標記的數據中提取模式,我們使用受限的Boltzman機器或自動編碼器。
在選擇深網時,請考慮以下幾點&負;
對於文本處理、情感分析、句法分析和名稱實體識別,我們使用遞歸網絡或遞歸神經張量網絡或RNTN;
對於任何在字符級運行的語言模型,我們都使用遞歸網。
對於圖像識別,我們使用深信度網絡DBN或卷積網絡。
對於目標識別,我們使用RNTN或卷積網絡。
對於語音識別,我們使用遞歸網絡。
一般來說,深度信念網絡和多層感知器都是很好的分類選擇。
對於時間序列分析,通常建議使用遞歸網。
神經網絡已經存在了50多年,但直到現在,它們才變得突出起來。原因是它們很難訓練;當我們試圖用反向傳播的方法訓練它們時,我們遇到了一個稱爲消失或爆炸梯度的問題。當這種情況發生時,訓練需要更長的時間,而準確度則居於次要地位。當訓練一個數據集時,我們不斷地計算成本函數,即一組標記的訓練數據的預測輸出和實際輸出之間的差異,然後通過調整權重和偏差值使成本函數最小化,直到得到最小值。訓練過程使用一個梯度,這個梯度是成本隨著權重或偏差值的變化而變化的速率。
Restricted Boltzman Networks or Autoencoders - RBNs
2006年,在解決梯度消失問題上取得了突破性進展。Geoff Hinton設計了一種新的策略,該策略導致了限制性Boltzman機器的發展——RBM,一種淺兩層網絡。
第一層是可見層,第二層是隱藏層。可見層中的每個節點都連接到隱藏層中的每個節點。網絡被稱爲受限的,因爲同一層中的兩個層不允許共享連接。
自動編碼器是將輸入數據編碼爲矢量的網絡。它們創建原始數據的隱藏或壓縮表示。向量在降維中是有用的;向量將原始數據壓縮成更小的基本維。自動編碼器與解碼器配對,允許根據其隱藏的表示重建輸入數據。
RBM在數學上等同於雙向翻譯。前向傳遞接受輸入並將其轉換爲一組對輸入進行編碼的數字。同時,一個向後的過程接受這組數字並將它們轉換回重構的輸入。訓練有素的網以高度的準確性進行後支撐。
在這兩個步驟中,權重和偏差都起著關鍵作用;它們有助於RBM解碼輸入之間的相互關係,並決定哪些輸入對檢測模式至關重要。通過向前和向後傳遞,訓練RBM用不同的權值和偏差重新構造輸入,直到輸入和構造儘可能接近爲止。成果管理制的一個有趣的方面是,數據無需標記。事實證明,這對於照片、視頻、聲音和傳感器數據等真實世界的數據集非常重要,而這些數據往往都是未標記的。RBM不需要人工標註數據,而是自動對數據進行排序;通過適當調整權重和偏差,RBM能夠提取重要特徵並重構輸入。RBM是特徵提取神經網絡家族的一部分,用於識別數據中的固有模式。這些也被稱爲自動編碼器,因爲它們必須編碼自己的結構。

Deep Belief Networks - DBNs
將RBMs與智能訓練方法相結合,形成了深度信任網絡(DBNs)。我們有一個新的模型,最終解決了梯度消失的問題。Geoff Hinton發明了RBMs和深度信念網作爲反向傳播的替代品。
DBN在結構上類似於MLP(多層感知器),但在訓練方面卻有很大的不同。正是這種培訓使DBNs能夠超越其膚淺的對手
DBN可以可視化爲一個RBM堆棧,其中一個RBM的隱藏層是其上面RBM的可見層。訓練第一個RBM以儘可能準確地重構其輸入。
將第一RBM的隱層作爲第二RBM的可見層,利用第一RBM的輸出對第二RBM進行訓練。這個過程被疊代,直到網絡中的每一層都得到訓練。
在DBN中,每個RBM學習整個輸入。DBN的全局工作原理是,隨著模型的緩慢改進(就像照相機鏡頭慢慢聚焦圖片一樣),對整個輸入進行連續微調。由於多層感知器MLP優於單一感知器,因此一組RBM優於單一RBM。
在此階段,RBMs檢測到數據中的固有模式,但沒有任何名稱或標籤。爲了完成DBN的訓練,我們必須在模式中引入標籤,並使用監督學習對網絡進行微調。
我們需要一個非常小的標記樣本集,這樣特徵和模式就可以與一個名稱相關聯。這一小部分有標籤的數據用於訓練。與原始數據集相比,這組標記數據可能非常小。
重量和偏倚略有改變,導致網絡對模式的感知發生了微小的變化,而且總的準確度通常略有提高。
與淺網相比,利用gpu可以在合理的時間內完成訓練,得到了非常精確的結果,並給出了消失梯度問題的解。
Generative Adversarial Networks - GANs
生成性對抗網絡是由兩個網絡組成的深層神經網絡,一個網絡對另一個網絡,因此被稱爲「對抗性」網絡。
2014年,蒙特婁大學(University of Montreal)的研究人員發表了一篇論文,介紹了GANs。Facebook的人工智慧專家YannLecun提到了GANs,他稱對抗性訓練是「過去10年裡ML最有趣的想法」
GANs的潛力是巨大的,因爲網絡掃描可以學習模擬任何數據分布。甘斯可以被教導在任何領域創造與我們相似的平行世界:圖像、音樂、演講、散文。他們在某種程度上是機器人藝術家,他們的作品令人印象深刻。
在GAN中,一個稱爲生成器的神經網絡生成新的數據實例,而另一個稱為鑑別器,則評估它們的真實性。
假設我們正在嘗試生成手寫數字,比如MNIST數據集中的數字,它取自真實世界。當從真實MNIST數據集中顯示實例時,鑑別器的工作是將它們識別爲真實的。
現在考慮一下GAN的以下步驟−
生成器網絡以隨機數的形式接收輸入並返回圖像。
生成的圖像與從實際數據集獲取的圖像流一起作為鑑別器網絡的輸入。
鑑別器接收真實和假的圖像,並返回機率,一個介於0和1之間的數字,1表示對真實性的預測,0表示假的。
所以你有一個雙反饋迴路;
鑑別器處於一個反饋迴路中,與我們所知道的圖像的基本真實性有關。
發生器與鑑別器處於反饋迴路中。
Recurrent Neural Networks - RNNs
RNN是一種數據可以向任何方向流動的神經網絡。這些網絡用於語言建模或自然語言處理(NLP)等應用。
RNNs的基本概念是利用序列信息。在一般的神經網絡中,所有的輸入和輸出都是相互獨立的。如果我們想預測一個句子中的下一個單詞,我們必須知道哪個單詞在它之前出現。
RNN被稱爲遞歸的,因爲它們對序列的每個元素重複相同的任務,而輸出是基於前面的計算。因此,可以說rnn有一個「內存」,它捕獲關於先前計算過的內容的信息。理論上,RNNs可以在很長的序列中使用信息,但實際上,它們只能回顧幾步。
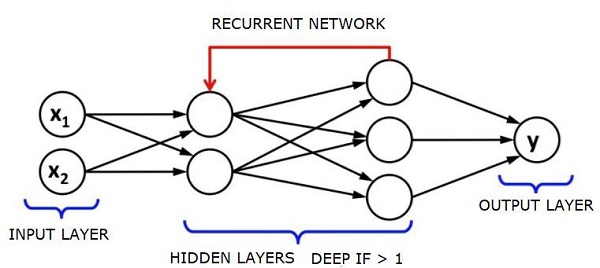
長期短期記憶網絡(LSTMs)是最常用的rnn。
與卷積神經網絡一起,RNNs被用作模型的一部分來生成未標記圖像的描述。這件事看起來很管用,真是太不可思議了。
Convolutional Deep Neural Networks - CNNs
如果我們增加一個神經網絡的層數以使它更深,它會增加網絡的複雜性,並允許我們對更複雜的函數進行建模。然而,權重和偏差的數量將成倍增加。事實上,學習這些難題對於普通的神經網絡來說是不可能的。這就引出了一個解決方案,卷積神經網絡。
CNNs被廣泛應用於計算機視覺,也被應用於自動語音識別的聲學建模。
卷積神經網絡背後的思想是通過圖像的「移動濾波器」的思想。該移動濾波器或卷積適用於節點的特定鄰域,例如,該鄰域可以是像素,其中所應用的濾波器是節點值的0.5 x負;
著名的研究人員YannLecun開創了卷積神經網絡。Facebook作爲面部識別軟體使用這些網絡。CNN一直是機器視覺項目的解決方案。卷積網絡有許多層。在Imagenet挑戰賽中,2015年,一台機器能夠在物體識別方面擊敗人類。
簡單地說,卷積神經網絡是一種多層神經網絡。這些層有時多達17個或更多,並且假設輸入數據是圖像。
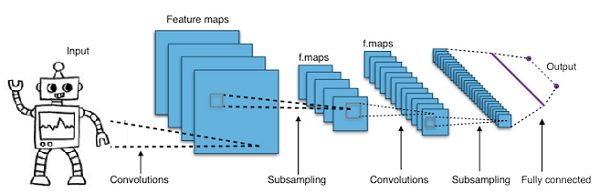
CNNs大大減少了需要調整的參數數量。因此,CNNs有效地處理了原始圖像的高維性。
Python Deep Learning - Fundamentals
在本章中,我們將探討Python深入學習的基本原理。
Deep learning models/algorithms
現在讓我們了解不同的深度學習模型/算法。
深度學習中的一些流行模式如下所示;
- Convolutional neural networks
- Recurrent neural networks
- Deep belief networks
- Generative adversarial networks
- Auto-encoders and so on
輸入和輸出用矢量或張量表示。例如,神經網絡可以具有將圖像中的單個像素RGB值表示爲向量的輸入。
位於輸入層和輸出層之間的神經元層稱爲隱藏層。當神經網絡試圖解決問題時,大部分工作都在這裡進行。仔細觀察隱藏層可以揭示網絡從數據中提取的許多特性。
神經網絡的不同結構是通過選擇哪些神經元連接到下一層的其他神經元而形成的。
Pseudocode for calculating output
下面是計算前向傳播神經網絡輸出的僞代碼;
- # node[] := array of topologically sorted nodes
- # An edge from a to b means a is to the left of b
- # If the Neural Network has R inputs and S outputs,
- # then first R nodes are input nodes and last S nodes are output nodes.
- # incoming[x] := nodes connected to node x
- # weight[x] := weights of incoming edges to x
對於每個神經元x,從左到右&負;
- if x <= R: do nothing # its an input node
- inputs[x] = [output[i] for i in incoming[x]]
- weighted_sum = dot_product(weights[x], inputs[x])
- output[x] = Activation_function(weighted_sum)
Training a Neural Network
我們現在將學習如何訓練神經網絡。在Python深度學習中,我們還將學習反向傳播算法和反向傳遞。
我們必須找到神經網絡權值的最佳值,才能得到期望的輸出。爲了訓練神經網絡,我們使用疊代梯度下降法。我們從權值的隨機初始化開始。在隨機初始化之後,我們用前向傳播過程對數據的某個子集進行預測,計算出相應的代價函數C,並以與dC/dw成比例的量更新每個權重w,即代價函數的導數w.r.t.權重。比例常數稱爲學習率。
利用反向傳播算法可以有效地計算梯度。反向傳播或反向道具的關鍵觀察是,由於存在著鏈式的分化規律,神經網絡中每個神經元的梯度可以用神經元的梯度來計算,它具有向外的邊緣。因此,我們向後計算梯度,即首先計算輸出層的梯度,然後計算最上面的隱藏層,然後計算前面的隱藏層,依此類推,以輸入層結束。
反向傳播算法主要使用計算圖的思想來實現,其中每個神經元被擴展到計算圖中的多個節點,並執行簡單的數學運算,如加法、乘法。計算圖的邊上沒有任何權重;所有權重都分配給節點,因此權重成爲它們自己的節點。然後在計算圖上運行反向傳播算法。計算完成後,更新只需要權重節點的漸變。其餘的漸變可以丟棄。
Gradient Descent Optimization Technique
一種常用的優化函數是「梯度下降」,它根據權重引起的誤差來調整權重
Gradient是slope的另一個名稱,slope在x-y圖上表示兩個變量之間的關係:在運行過程中的上升、在時間變化過程中距離的變化等。在這種情況下,slope是網絡誤差和單個權重之間的比率;即,誤差如何隨著權重的變化而變化。
更準確地說,我們想找出哪種重量產生的誤差最小。我們希望找到正確表示輸入數據中包含的信號的權重,並將其轉換爲正確的分類。
當神經網絡學習時,它會慢慢地調整許多權值,以便它們能正確地將信號映射到意義上。網絡誤差與這些權重中的每一個之間的比率是一個導數dE/dw,它計算權重的微小變化導致誤差微小變化的程度。
在一個包含許多變換的深層網絡中,每個權值只是一個因素;權值的信號通過激活並在多個層上求和,因此我們使用微積分的鏈式規則通過網絡激活和輸出進行計算。這就引出了所討論的權值,以及它與整體誤差的關係。
給定兩個變量,誤差和權重,通過第三個變量激活傳遞權重。我們可以通過首先計算激活的變化如何影響錯誤的變化,以及權重的變化如何影響激活的變化來計算權重的變化如何影響錯誤的變化。
深度學習的基本思想就是:根據模型產生的誤差調整模型的權重,直到不能再減少誤差爲止。
梯度值越小,深網訓練越慢;梯度值越高,深網訓練越快。培訓中的任何不準確都會導致輸出不準確。將網絡從輸出訓練回輸入的過程稱爲反向傳播或反向支撐。我們知道正向傳播是從輸入開始的,並且是向前的。Back prop執行從右到左的反向/反向計算漸變。
每次我們計算一個梯度時,我們都會使用到那個點之前的所有梯度。
讓我們從輸出層的一個節點開始。邊使用該節點處的漸變。當我們回到隱藏層,它變得更加複雜。介於0和1之間的兩個數字的乘積給出一個較小的數字。梯度值越來越小,因此背道具需要花費大量的時間來訓練,精度受到影響。
Challenges in Deep Learning Algorithms
無論是淺層神經網絡還是深層神經網絡,都存在著一定的挑戰,如過擬合和計算時間。dnn會受到過度擬合的影響,因爲它使用了附加的抽象層,使它們能夠在訓練數據中建立罕見的依賴關係模型。
在訓練過程中,運用了退學、提前停站、數據增強、遷移學習等正則化方法來對抗過度擬合。退出正則化在訓練過程中隨機從隱藏層中忽略單元,這有助於避免罕見的依賴。DNNs考慮了多個訓練參數,如大小,即每層的層數和單元數,學習率和初始權值。由於時間和計算資源的高成本,尋找最優參數並不總是可行的。一些技巧,如批處理,可以加快計算速度。由於所需的矩陣和矢量計算在gpu上得到了很好的執行,gpu強大的處理能力極大地幫助了訓練過程。
Dropout
輟學是一種流行的神經網絡正則化技術。深層神經網絡特別容易過度擬合。
現在讓我們看看輟學是什麼以及它是如何運作的。
用深度學習的先驅之一傑弗里·辛頓(Geoffrey Hinton)的話來說,「如果你有一個深度神經網絡,而且它並不過分合適,那麼你可能應該使用一個更大的網絡,並使用輟學」。
輟學是一種技術,在每次梯度下降疊代過程中,我們會丟棄一組隨機選擇的節點。這意味著我們隨機忽略一些節點,就好像它們不存在一樣。
每一個神經元以q的機率保持,以1-q的機率隨機下降。在神經網絡中,每一層的q值可能不同。對於隱藏層,值爲0.5,對於輸入層,值爲0,可以很好地處理各種任務。
在評估和預測期間,不使用輟學。每個神經元的輸出乘以q,這樣到下一層的輸入具有相同的期望值。
輟學背後的想法是這樣的,在一個沒有輟學規則化的神經網絡中,神經元之間會產生相互依賴關係,從而導致過度擬合。
Implementation trick
在TensorFlow和Pytorch等庫中,通過將隨機選擇的神經元的輸出保持爲0來實現輟學。也就是說,雖然神經元存在,但其輸出被覆蓋爲0。
Early Stopping
我們使用一種叫做梯度下降的疊代算法訓練神經網絡。
提前停止的想法是直觀的;當錯誤開始增加時,我們停止訓練。這裡,所謂誤差,是指在驗證數據上測量的誤差,它是用於調整超參數的訓練數據的一部分。在這種情況下,超參數是停止條件。
Data Augmentation
通過使用現有數據並對其應用某些轉換來增加我們擁有的數據量或增加它的過程。所使用的確切轉換取決於我們打算完成的任務。此外,幫助神經網絡的轉換依賴於它的結構。
例如,在許多計算機視覺任務中,例如對象分類,一種有效的數據增強技術是添加新的數據點,這些數據點是原始數據的裁剪或翻譯版本。
當計算機接受圖像作爲輸入時,它接受一個像素值數組。假設整個圖像左移15像素。我們在不同的方向上應用了許多不同的移位,結果得到了一個比原始數據集大很多倍的擴展數據集。
Transfer Learning
接受預先訓練的模型並用我們自己的數據集「微調」模型的過程稱爲轉移學習。有幾種方法可以做到這一點;
我們在一個大數據集上訓練預先訓練的模型。然後,我們移除網絡的最後一層,並將其替換爲具有隨機權重的新層。
然後凍結所有其他層的權重,並正常訓練網絡。在這裡凍結圖層並不會改變梯度下降或優化過程中的權重。
這背後的概念是,預先訓練的模型將充當特徵提取器,只有最後一層將在當前任務上進行訓練。
Computational Graphs
反向傳播通過使用計算圖在諸如Tensorflow、Torch、Theano等深度學習框架中實現。更重要的是,理解計算圖上的反向傳播結合了幾種不同的算法及其變化,如時間反向傳播和具有共享權重的反向傳播。一旦所有東西都轉換成計算圖,它們仍然是相同的算法,只是計算圖上的反向傳播。
What is Computational Graph
計算圖被定義爲節點對應於數學運算的有向圖。計算圖是表示和計算數學表達式的一種方法。
例如,這裡有一個簡單的數學方程&負;
$$p = x+y$$
我們可以畫出上述方程的計算圖如下。
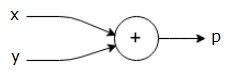
上面的計算圖有一個加法節點(帶有「+」符號的節點),它有兩個輸入變量x和y以及一個輸出變量q。
讓我們再舉一個稍微複雜一點的例子。我們有以下方程式。
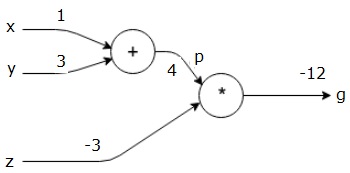
$$g = \left (x+y \right ) \ast z $$
上面的方程由下面的計算圖表示。
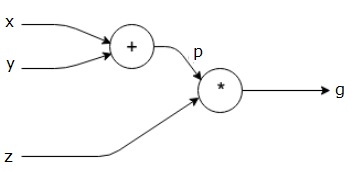
Computational Graphs and Backpropagation
計算圖和反向傳播都是神經網絡深度學習的重要核心概念。
Forward Pass
正向傳遞是計算圖表示的數學表達式的值的計算過程。執行forward pass意味著我們將變量的值從左(輸入)向右(輸出所在)正向傳遞。
讓我們考慮一個例子,給出所有輸入的一些值。假設,爲所有輸入提供以下值。
$$x=1, y=3, z=−3$$
通過將這些值賦給輸入,我們可以執行前向傳遞,並爲每個節點上的輸出獲取以下值。
首先,我們使用x=1和y=3的值,得到p=4。
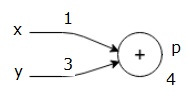
然後我們用p=4和z=-3得到g=-12。我們從左到右,向前走。
Objectives of Backward Pass
在反向過程中,我們的目的是計算每個輸入相對於最終輸出的梯度。這些梯度對於利用梯度下降訓練神經網絡是必不可少的。
例如,我們需要以下漸變。
Desired gradients
$$\frac{\partial x}{\partial f}, \frac{\partial y}{\partial f}, \frac{\partial z}{\partial f}$$
Backward pass (backpropagation)
我們通過找到最終輸出相對於最終輸出(本身)的導數來開始反向傳遞。因此,它將導致恆等式推導,並且該值等於1。
$$\frac{\partial g}{\partial g} = 1$$
我們的計算圖如下所示;
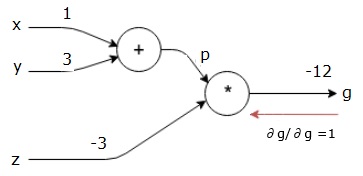
接下來,我們將通過「*」操作執行反向傳遞。我們將計算p和z的梯度,因爲g=p*z,我們知道&;
$$\frac{\partial g}{\partial z} = p$$
$$\frac{\partial g}{\partial p} = z$$
我們已經知道了z和p的值。因此,我們得到&負;
$$\frac{\partial g}{\partial z} = p = 4$$
and
$$\frac{\partial g}{\partial p} = z = -3$$
我們要計算x和y的梯度;
$$\frac{\partial g}{\partial x}, \frac{\partial g}{\partial y}$$
然而,我們想有效地做到這一點(儘管x和g在這個圖中只相差兩個跳,但假設它們彼此之間確實很遠)。爲了有效地計算這些值,我們將使用微分鏈規則。根據鏈式法則,我們有&;
$$\frac{\partial g}{\partial x}=\frac{\partial g}{\partial p}\ast \frac{\partial p}{\partial x}$$
$$\frac{\partial g}{\partial y}=\frac{\partial g}{\partial p}\ast \frac{\partial p}{\partial y}$$
但是我們已經知道dg/dp=-3,dp/dx和dp/dy很容易,因爲p直接依賴於x和y;
$$p=x+y\Rightarrow \frac{\partial x}{\partial p} = 1, \frac{\partial y}{\partial p} = 1$$
因此,我們得到&負;
$$\frac{\partial g} {\partial f} = \frac{\partial g} {\partial p}\ast \frac{\partial p} {\partial x} = \left ( -3 \right ).1 = -3$$
另外,對於輸入y&負;
$$\frac{\partial g} {\partial y} = \frac{\partial g} {\partial p}\ast \frac{\partial p} {\partial y} = \left ( -3 \right ).1 = -3$$
反向執行此操作的主要原因是,當我們必須計算x處的梯度時,我們只使用已計算的值和dq/dx(節點輸出相對於同一節點輸入的導數)。我們使用本地信息來計算全局值。
Steps for training a neural network
按照以下步驟訓練神經網絡&負;
對於數據集中的數據點x,我們用x作爲輸入進行正向傳遞,並計算出成本c作爲輸出。
我們從c開始反向傳遞,並計算圖中所有節點的梯度。這包括表示神經網絡權重的節點。
然後我們通過做W=W-學習率*梯度來更新權重。
我們重複此過程,直到滿足停止標準。
Python Deep Learning - Applications
深度學習在計算機視覺、語言翻譯、圖像字幕、音頻轉錄、分子生物學、語音識別、自然語言處理、自動駕駛汽車、腦瘤檢測、實時語音翻譯、音樂創作、自動遊戲播放等應用中取得了良好的效果。
深度學習是繼機器學習之後的又一個更先進的實現方式。目前,它正朝著成爲一個行業標準的方向發展,在處理原始的非結構化數據時,它有望成爲遊戲規則的改變者。
深度學習是目前解決各種現實問題的最佳解決方案之一。開發人員正在開發人工智慧程序,而不是使用以前給定的規則,從示例中學習解決複雜任務。隨著深度學習被許多數據科學家所使用,深度神經網絡正在提供更加精確的結果。
其思想是通過增加每個網絡的訓練層數量來開發深層神經網絡;機器學習更多的數據,直到儘可能精確。開發人員可以使用深度學習技術來實現複雜的機器學習任務,並訓練人工智慧網絡具有高水平的感知識別能力。
深度學習在計算機視覺中很受歡迎。這裡所完成的任務之一是圖像分類,其中給定的輸入圖像被分類爲貓、狗等,或者被分類爲最能描述圖像的類或標籤。作爲人類,我們很早就學會了如何完成這項任務,並且擁有快速識別模式、從先前的知識中歸納、適應不同圖像環境的技能。
Libraries and Frameworks
在本章中,我們將把深入學習與不同的庫和框架聯繫起來。
Deep learning and Theano
如果我們想開始編碼一個深層神經網絡,最好我們有一個不同的框架,比如Theano、TensorFlow、Keras、PyTorch等,是如何工作的。
Theano是python庫,它提供了一組函數,用於構建在我們的機器上快速訓練的深層網絡。
Theano是在加拿大蒙特婁大學(University of Montreal)由一位深度網絡先驅Yoshua Bengio領導下開發的。
它允許我們定義和計算帶有向量和矩陣的數學表達式,這些向量和矩陣是數字的矩形陣列。
從技術上講,神經網絡和輸入數據都可以表示爲矩陣,所有標準的網絡操作都可以重新定義爲矩陣操作。這一點很重要,因爲計算機可以很快地執行矩陣運算。
我們可以並行處理多個矩陣值,如果我們用這種底層結構構建一個神經網絡,我們就可以用一台帶有GPU的機器在一個合理的時間窗內訓練龐大的網絡。
然而,如果我們使用天網,我們必須從頭開始建立深網。庫沒有提供創建特定類型的deep net的完整功能。
相反,我們必須對深網的各個方面進行編碼,比如模型、層、激活、訓練方法和任何防止過度擬合的特殊方法。
不過,好消息是,Theano允許在矢量化函數之上構建我們的實現,從而爲我們提供一個高度優化的解決方案。
還有許多其他庫擴展了ano的功能。TensorFlow和Keras可以與ano一起用作後端。
Deep Learning with TensorFlow
Googles TensorFlow是一個python庫。該圖書館是建設商業級深度學習應用的絕佳選擇。
TensorFlow源於另一個圖書館DistFeedge V2,它是Google Brain項目的一部分。該庫旨在擴展機器學習的可移植性,以便研究模型可以應用於商業級應用。
與Theano庫非常相似,tensor flow是基於計算圖的,其中一個節點表示持久數據或數學運算,而邊表示節點之間的數據流,這是一個多維數組或tensor;因此,TensorFlow的名稱是
一個操作或一組操作的輸出作爲下一個操作的輸入。
儘管TensorFlow是爲神經網絡設計的,但它也適用於其他可以將計算建模爲數據流圖的網絡。
TensorFlow還使用了一些來自Theano的特性,如公共和子表達式消除、自微分、共享和符號變量。
利用卷積網、自動編碼器、RNTN、RNN、RBM、DBM/MLP等張量流可以構造不同類型的深網。
但是,TensorFlow中不支持超參數配置。對於此功能,我們可以使用Keras。
Deep Learning and Keras
Keras是一個強大的易於使用的Python庫,用於開發和評估深度學習模型。
它有一個極簡的設計,允許我們建立一個網絡一層一層,訓練它,並運行它。
它封裝了高效的數值計算庫Theano和TensorFlow,允許我們用幾行代碼定義和訓練神經網絡模型。
它是一個高級的神經網絡API,有助於深度學習和人工智慧的廣泛應用。它運行在許多較低級別的庫之上,包括TensorFlow、Theano等。Keras代碼是可移植的;我們可以在Keras中實現一個神經網絡,使用ano或TensorFlow作爲後端,代碼沒有任何變化。
Python Deep Learning - Implementations
在這個深度學習的實現中,我們的目標是預測某家銀行的客戶流失或客戶流失數據-哪些客戶可能離開此銀行服務。使用的數據集相對較小,包含10000行14列。我們正在使用Anaconda發行版,以及Theano、TensorFlow和Keras等框架。路緣石建在Tensorflow和Theano的頂部,Tensorflow和Theano作爲路緣石的後端。
# Artificial Neural Network # Installing Theano pip install --upgrade theano # Installing Tensorflow pip install –upgrade tensorflow # Installing Keras pip install --upgrade keras
Step 1: Data preprocessing
In[]:
# Importing the libraries
import numpy as np
import matplotlib.pyplot as plt
import pandas as pd
# Importing the database
dataset = pd.read_csv('Churn_Modelling.csv')
Step 2
我們創建數據集特徵和目標變量的矩陣,即列14,標記爲「Exited」。
數據的初始外觀如下所示;
In[]: X = dataset.iloc[:, 3:13].values Y = dataset.iloc[:, 13].values X
Output
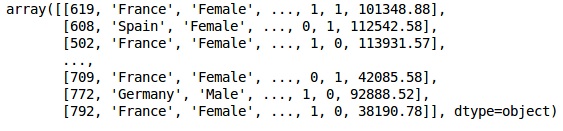
Step 3
Y
Output
array([1, 0, 1, ..., 1, 1, 0], dtype = int64)
Step 4
我們通過對字符串變量進行編碼使分析更簡單。我們使用ScikitLearn函數「LabelEncoder」自動對列中的不同標籤進行編碼,其值介於0到n_classes-1之間。
from sklearn.preprocessing import LabelEncoder, OneHotEncoder labelencoder_X_1 = LabelEncoder() X[:,1] = labelencoder_X_1.fit_transform(X[:,1]) labelencoder_X_2 = LabelEncoder() X[:, 2] = labelencoder_X_2.fit_transform(X[:, 2]) X
Output
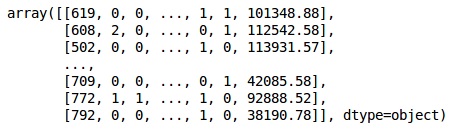
在上述輸出中,國家名稱替換爲0、1和2;男性和女性替換爲0和1。
Step 5
標記編碼數據
我們使用相同的ScikitLearn庫和另一個名爲onehotecoder的函數來傳遞創建虛擬變量的列號。
onehotencoder = OneHotEncoder(categorical features = [1]) X = onehotencoder.fit_transform(X).toarray() X = X[:, 1:] X
現在,前兩列代表國家,第四列代表性別。
Output
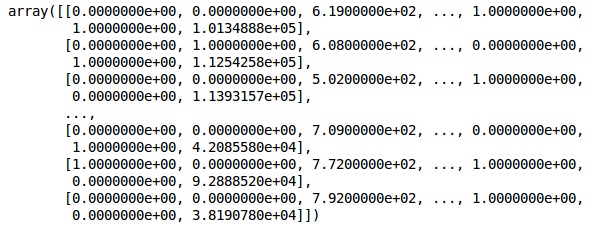
我們總是將數據分爲訓練和測試兩部分,對訓練數據進行模型訓練,然後對測試數據進行模型精度檢驗,這有助於評估模型的效率。
Step 6
我們使用ScikitLearn的train_test_split函數將數據分成訓練集和測試集。我們把列車與測試的比例保持在80:20。
#Splitting the dataset into the Training set and the Test Set from sklearn.model_selection import train_test_split X_train, X_test, y_train, y_test = train_test_split(X, y, test_size = 0.2)
有些變量的值以千爲單位,而有些變量的值以十或一爲單位。我們對數據進行縮放,使其更具代表性。
Step 7
在這段代碼中,我們使用StandardScaler函數擬合和轉換訓練數據。我們將縮放標準化,以便使用相同的擬合方法轉換/縮放測試數據。
# Feature Scaling
fromsklearn.preprocessing import StandardScaler sc = StandardScaler() X_train = sc.fit_transform(X_train) X_test = sc.transform(X_test)
Output
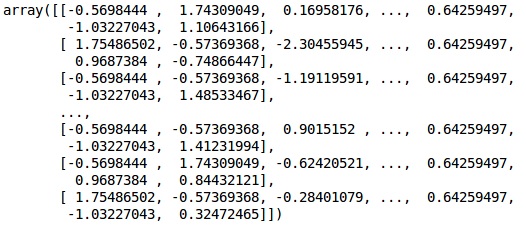
The data is now scaled properly. Finally, we are done with our data pre-processing. Now,we will start with our model.
Step 8
We import the required Modules here. We need the Sequential module for initializing the neural network and the dense module to add the hidden layers.
# Importing the Keras libraries and packages import keras from keras.models import Sequential from keras.layers import Dense
Step 9
我們將模型命名爲分類器,因爲我們的目標是對客戶流失進行分類。然後使用順序模塊進行初始化。
#Initializing Neural Network classifier = Sequential()
Step 10
我們使用密集函數逐個添加隱藏層。在下面的代碼中,我們將看到許多參數。
我們的第一個參數是輸出。這是我們添加到該層的節點數。init是隨機梯度下降的初始化。在神經網絡中,我們給每個節點分配權重。在初始化時,權值應該接近於零,我們使用均勻函數隨機初始化權值。因爲模型不知道輸入變量的數目,所以只需要第一層輸入參數。這裡輸入變量的總數是11。在第二層,模型自動從第一個隱藏層知道輸入變量的數量。
執行以下代碼行以添加輸入層和第一個隱藏層−
classifier.add(Dense(units = 6, kernel_initializer = 'uniform', activation = 'relu', input_dim = 11))
執行以下代碼行以添加第二個隱藏層−
classifier.add(Dense(units = 6, kernel_initializer = 'uniform', activation = 'relu'))
執行以下代碼行以添加輸出層−
classifier.add(Dense(units = 1, kernel_initializer = 'uniform', activation = 'sigmoid'))
Step 11
編制人工神經網絡
到目前爲止,我們已經在分類器中添加了多個層。我們現在將使用compile方法編譯它們。在最終編譯控制中添加的參數完成了神經網絡。因此,在這一步中我們需要小心。
以下是對論點的簡要解釋。
第一個參數是優化器。這種算法稱爲隨機梯度下降(SGD)。在這裡,我們使用幾種類型中的一種,稱爲「Adam優化器」。SGD取決於損耗,所以我們的第二個參數是損耗。如果因變量是二進位的,我們使用對數損失函數稱爲「二進位交叉熵」,如果因變量在輸出中有兩個以上的類別,則使用「分類交叉熵」。我們希望基於精度提高神經網絡的性能,所以我們添加了度量值作爲精度。
# Compiling Neural Network classifier.compile(optimizer = 'adam', loss = 'binary_crossentropy', metrics = ['accuracy'])
Step 12
在此步驟中需要執行許多代碼。
Fitting the ANN to the Training Set
我們現在根據訓練數據訓練我們的模型。我們使用擬合方法來擬合我們的模型。爲了提高模型的效率,我們還對權重進行了優化。爲此,我們必須更新權重。Batch size是更新權重後的觀察數。Epoch是疊代的總數。採用試錯法選擇批量大小和曆元值。
classifier.fit(X_train, y_train, batch_size = 10, epochs = 50)
Making predictions and evaluating the model
# Predicting the Test set results y_pred = classifier.predict(X_test) y_pred = (y_pred > 0.5)
Predicting a single new observation
# Predicting a single new observation """Our goal is to predict if the customer with the following data will leave the bank: Geography: Spain Credit Score: 500 Gender: Female Age: 40 Tenure: 3 Balance: 50000 Number of Products: 2 Has Credit Card: Yes Is Active Member: Yes
Step 13
預測測試集結果
預測結果會給你客戶離開公司的可能性。我們將把這個機率轉換成二進位0和1。
# Predicting the Test set results y_pred = classifier.predict(X_test) y_pred = (y_pred > 0.5)
new_prediction = classifier.predict(sc.transform (np.array([[0.0, 0, 500, 1, 40, 3, 50000, 2, 1, 1, 40000]]))) new_prediction = (new_prediction > 0.5)
Step 14
This is the last step where we evaluate our model performance. We already have original results and thus we can build confusion matrix to check the accuracy of our model.
Making the Confusion Matrix
from sklearn.metrics import confusion_matrix cm = confusion_matrix(y_test, y_pred) print (cm)
Output
loss: 0.3384 acc: 0.8605 [ [1541 54] [230 175] ]
From the confusion matrix, the Accuracy of our model can be calculated as −
Accuracy = 1541+175/2000=0.858
我們達到了85.8%的準確度,這是很好的。
The Forward Propagation Algorithm
在本節中,我們將學習如何編寫代碼來爲一個簡單的神經網絡進行正向傳播(預測)&負;
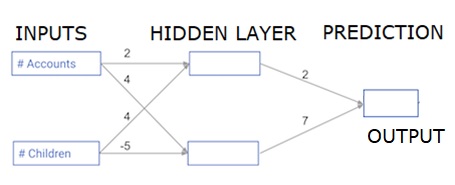
每個數據點都是客戶。第一個輸入是他們有多少帳戶,第二個輸入是他們有多少孩子。該模型將預測用戶在下一年進行多少交易。
輸入數據作爲輸入數據預加載,權重在稱爲權重的字典中。隱藏層中第一個節點的權重數組分別爲權重['node_0'],隱藏層中第二個節點的權重數組分別爲權重['node_1']。
輸入到輸出節點的權重以權重形式提供。
The Rectified Linear Activation Function
「激活功能」是在每個節點工作的功能。它將節點的輸入轉換爲一些輸出。
校正線性激活函數(稱爲ReLU)廣泛應用於高性能網絡。此函數將單個數字作爲輸入,如果輸入爲負,則返回0;如果輸入爲正,則輸入爲輸出。
下面是一些例子;
- relu(4) = 4
- relu(-2) = 0
我們填寫relu()函數的定義−
- We use the max() function to calculate the value for the output of relu().
- We apply the relu() function to node_0_input to calculate node_0_output.
- We apply the relu() function to node_1_input to calculate node_1_output.
import numpy as np
input_data = np.array([-1, 2])
weights = {
'node_0': np.array([3, 3]),
'node_1': np.array([1, 5]),
'output': np.array([2, -1])
}
node_0_input = (input_data * weights['node_0']).sum()
node_0_output = np.tanh(node_0_input)
node_1_input = (input_data * weights['node_1']).sum()
node_1_output = np.tanh(node_1_input)
hidden_layer_output = np.array(node_0_output, node_1_output)
output =(hidden_layer_output * weights['output']).sum()
print(output)
def relu(input):
'''Define your relu activation function here'''
# Calculate the value for the output of the relu function: output
output = max(input,0)
# Return the value just calculated
return(output)
# Calculate node 0 value: node_0_output
node_0_input = (input_data * weights['node_0']).sum()
node_0_output = relu(node_0_input)
# Calculate node 1 value: node_1_output
node_1_input = (input_data * weights['node_1']).sum()
node_1_output = relu(node_1_input)
# Put node values into array: hidden_layer_outputs
hidden_layer_outputs = np.array([node_0_output, node_1_output])
# Calculate model output (do not apply relu)
odel_output = (hidden_layer_outputs * weights['output']).sum()
print(model_output)# Print model output
Output
0.9950547536867305 -3
Applying the network to many Observations/rows of data
在本節中,我們將學習如何定義名爲predict_with_network()的函數。此函數將生成多個數據觀測的預測,從上述網絡獲取作爲輸入數據。正在使用上述網絡中給定的權重。relu()函數定義也正在使用。
讓我們定義一個名爲predict_with_network()的函數,它接受兩個參數-input_data_row和weights-並從網絡返回一個預測作爲輸出。
我們計算每個節點的輸入和輸出值,將它們存儲爲:node_0_輸入、node_0_輸出、node_1_輸入和node_1_輸出。
爲了計算節點的輸入值,我們將相關數組相乘並計算它們的和。
要計算節點的輸出值,我們將relu()函數應用於節點的輸入值。我們使用「for循環」來疊代輸入的數據;
我們還使用predict_with_network()爲input_data-input_data行的每一行生成預測。我們還將每個預測附加到結果中。
# Define predict_with_network() def predict_with_network(input_data_row, weights): # Calculate node 0 value node_0_input = (input_data_row * weights['node_0']).sum() node_0_output = relu(node_0_input) # Calculate node 1 value node_1_input = (input_data_row * weights['node_1']).sum() node_1_output = relu(node_1_input) # Put node values into array: hidden_layer_outputs hidden_layer_outputs = np.array([node_0_output, node_1_output]) # Calculate model output input_to_final_layer = (hidden_layer_outputs*weights['output']).sum() model_output = relu(input_to_final_layer) # Return model output return(model_output) # Create empty list to store prediction results results = [] for input_data_row in input_data: # Append prediction to results results.append(predict_with_network(input_data_row, weights)) print(results)# Print results
Output
[0, 12]
這裡我們使用relu函數,其中relu(26)=26,relu(-13)=0,依此類推。
Deep multi-layer neural networks
在這裡,我們編寫代碼來做兩個隱藏層的神經網絡的正向傳播。每個隱藏層有兩個節點。輸入數據已預加載爲輸入數據。第一個隱藏層中的節點稱爲node_0_0和node_0_1。
它們的權重分別預加載爲權重['node_0_0']和權重['node_0_1']。
第二個隱藏層中的節點稱爲node_1_0和node_1_1。它們的權重分別預加載爲權重['node_1_0']和權重['node_1_1']。
然後,我們使用預先加載爲權重['output']的權重從隱藏節點創建模型輸出。
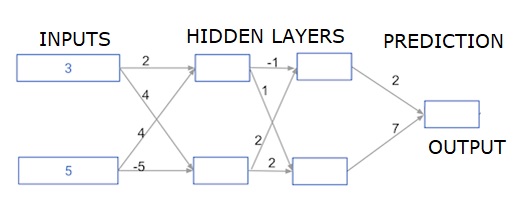
我們使用節點的權重和給定的輸入數據計算節點的輸入。然後應用relu()函數獲取node_0_0_輸出。
我們對node_0_1_輸入執行上述操作,以獲取node_0_1_輸出。
我們使用節點的權重和第一個隱藏層的輸出計算節點的輸入。然後我們應用relu()函數來獲取node_1_0_輸出。
我們對node_1_1_1_輸入執行上述操作,以獲得node_1_1_1_輸出。
我們使用權重[「output」]和來自第二隱藏層hidden_1_outputs數組的輸出計算模型_輸出。我們不對該輸出應用relu()函數。